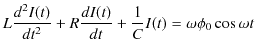Chapter12 交流

12.1 交流発電機

家庭で使用されている電気は交流です．交流は，電流の向きが周期的に交互に入れ替わります．抵抗一つと交流電源一つからなる簡単な交流回路において，一方の向きを正の向きと約束すると，抵抗の両端の電位差や流れる電流を表す横軸時間のグラフは正弦曲線になります．正弦曲線になる理由は，交流電源の仕組みを考えると理解できます．

　交流電源は通常，交流発電機でできています．その原理を説明します．交流発電機では，一様な磁束密度 $ B[T]$ の中で外から力を加え，コイルを一定の角速度 $ \omega[rad/s]$ で回転させます．（簡単のため，コイルはひと巻きであるとします．また，コイルが磁束密度と垂直な状態で時刻 $ t=0[s]$ とします．）コイルの面積を $ S[m^{2}]$ とすると，コイルの磁束密度に垂直な面積は， $ S\cdot\cos\omega t [m^{2}]$ と周期的に変化します．（図を見て下さい．）

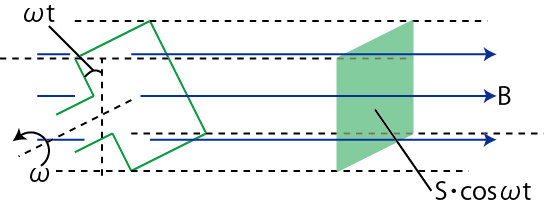
交流発電機

Figure12.1: 交流発電機

このとき，コイルを貫く磁束 $ \Phi(t)[Wb]$ は，

$\displaystyle \Phi(t)=B\cdot S\cos\omega t$

と周期的に変化します．磁束が変化すると電磁誘導が起こり，誘導起電力が発生します．ファラデーの電磁誘導の法則，

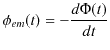
$\displaystyle \phi_{em}(t)=-\dfrac{d\Phi(t)}{dt}$

より，

$\displaystyle \phi(t)$ $\displaystyle =-\dfrac{d}{dt}(BS\cos\omega t)$    
  $\displaystyle =-BS(-\omega\sin\omega t)$    
  $\displaystyle =BS\omega\sin\omega t$    

となります．ここで，起電力の絶対値の最大値を， $ \phi_{0}\equiv BS\omega$ とおくと，

$\displaystyle \phi(t)=\phi_{0}\sin\omega t$

と交流発電機の起電力を表す式が求められます．確かに，グラフは正弦曲線になることが確認されます．

　交流の起電力の周期 $ T[s]$ は，コイルの回転の周期に等しくなっています．交流の $ 1[s]$ 当たりの振動の回数，

$\displaystyle f=\dfrac{1}{T}$

を周波数といいます．周波数 $ f$ の単位は $ [Hz($ヘルツ$ )(=1/s)]$ です．また， $ \omega[rad/s]$ は交流の角周波数といいますが，コイルの回転の角速度に等しくなっています．ここで，

$\displaystyle \omega=\dfrac{2\pi}{T}=2\pi f$

の関係があります．

 

12.2 R回路

交流電源に抵抗を1つ繋いだだけの回路をR回路と呼ぶことにします．前のSectionの交流発電機の起電力がそのまま抵抗にかかります．すなわち，抵抗の電位差 $ \phi(t)[V]$ は，

$\displaystyle \phi(t)=\phi_{0}\sin\omega t$

です．電位差が変化する場合でも，その瞬間その瞬間の電位差と電流を考えることができます．その瞬間その瞬間の電位差や電流の値を瞬時値といいます．電位差と電流の瞬時値について，オームの法則が成立するので，抵抗を流れる電流 $ I(t)[A]$ は，

$\displaystyle I(t)$ $\displaystyle =\dfrac{\phi(t)}{R}$    
  $\displaystyle =\dfrac{\phi_{0}}{R}\sin\omega t$    

となります．ここで，電流の最大値を，

$\displaystyle I_{0}\equiv\dfrac{\phi_{0}}{R}$

とおくと，

$\displaystyle I(t)=I_{0}\sin\omega t$

となります．ここで注意することは，電位差と電流の位相が揃っていることと，電位差の最大値と電流の最大値の間にもオームの法則が成立することです．

　抵抗に交流が流れるとき，ジュール熱が発生します．その電力の瞬時値 $ P(t)[W]$ は時間とともに変化しますが，次のようになります．

$\displaystyle P(t)$ $\displaystyle =I(t)\phi(t)$    
  $\displaystyle =I_{0}\sin\omega t\cdot\phi_{0}\sin\omega t$    
  $\displaystyle =I_{0}\phi_{0}\sin^{2}\omega t$    

故に，電力の時間平均値を $ P[W]$ とすると，周期を $ T[s]$ として，

$\displaystyle P$ $\displaystyle =\dfrac{1}{T}\int_{0}^{T}dt\cdot I_{0}\phi_{0}\sin^{2}\omega t$    
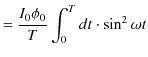  $\displaystyle =\dfrac{I_{0}\phi_{0}}{T}\int_{0}^{T}dt\cdot\sin^{2}\omega t$    
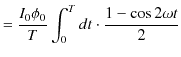  $\displaystyle =\dfrac{I_{0}\phi_{0}}{T}\int_{0}^{T}dt\cdot\dfrac{1-\cos⁡2\omega t}{2}$    
  $\displaystyle =\dfrac{I_{0}\phi_{0}}{T}[\dfrac{1}{2}t-\dfrac{\sin⁡2\omega t}{4\omega}]_{0}^{T}$    
  $\displaystyle =\dfrac{I_{0}\phi_{0}}{T}\cdot\dfrac{T}{2}$    
  $\displaystyle =\dfrac{1}{2}I_{0}\phi_{0}$    

となります．ここで，

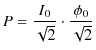
$\displaystyle P=\dfrac{I_{0}}{\sqrt{2}}\cdot\dfrac{\phi_{0}}{\sqrt{2}}$

と変形し，電流や電位差の実際上，電力に寄与する量として，

$\displaystyle I_{e}$ $\displaystyle \equiv\dfrac{I_{0}}{\sqrt{2}}$    
$\displaystyle \phi_{e}$ $\displaystyle \equiv\dfrac{\phi_{0}}{\sqrt{2}}$    

を定義します．これらを電流や電位差の実効値といいます．このとき，

$\displaystyle P=I_{e}\phi_{e}$

の関係が成立することがわかります．また，これらの実効値の間には，

$\displaystyle \dfrac{\phi_{e}}{I_{e}}$ $\displaystyle =\dfrac{\dfrac{\phi_{0}}{\sqrt{2}}}{\dfrac{I_{0}}{\sqrt{2}}}$    
  $\displaystyle =\dfrac{\phi_{0}}{I_{0}}$    
  $\displaystyle =R$    

より，実効値に関するオームの法則，

$\displaystyle \phi_{e}=RI_{e}$

が成立します．結局，R回路では，瞬時値，最大値と実効値の3種類の量に関して，オームの法則が成立することがわかりました．

 

12.3 L回路

交流電源にコイルを1個だけ繋いだ回路をL回路と呼ぶことにします．コイルに交流が流れるとき，自己誘導の起電力がコイルに生じます．この起電力は電流の変化を妨げる向きに発生するので，交流電流を抑制する働きをもちます．L回路において，コイルの導線の抵抗は無視できるものとします．このとき，コイルの両端の電位差は $ 0[V]$ になります．つまり，交流電源の起電力 $ \phi(t)[V]$ と，自己誘導の起電力，

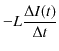
$\displaystyle -L\dfrac{\Delta I(t)}{\Delta t}$

がつりあうことになります．すなわち，

  $\displaystyle \phi(t)+(-L\dfrac{\Delta I(t)}{\Delta t})=0$    
% latex2html id marker 1762 $\displaystyle \therefore$ $\displaystyle \phi(t)=L\dfrac{\Delta I(t)}{\Delta t}$    

が成立します．時間間隔が限りなく 0 近づく極限をとると，

$\displaystyle \phi(t)=L\dfrac{dI(t)}{dt}$

となります．ここで，コイルを流れる交流電流が，

$\displaystyle I(t)=I_{0}\sin\omega t$

と変化したとすると，コイルに交流電源からかかる電位差 $ \phi(t)[V]$ は，

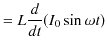$\displaystyle \phi(t)$ $\displaystyle =L\dfrac{d}{dt}(I_{0}\sin⁡\omega t)$    
  $\displaystyle =\omega LI_{0}\cos\omega t$    

となります．ここで，電位差の最大値を， $ \phi_{0}\equiv\omega LI_{0}$ とおき，三角関数の公式を使うと，

$\displaystyle \phi(t)=\phi_{0}\sin(\omega t+\dfrac{\pi}{2})$

となります．つまり，電流の位相は電位差の位相より， $ \frac{\pi}{2}[rad]$ だけ小さい（遅れている）ことがわかります．（位相のずれのため，L回路では，瞬時値に関するオームの法則は成立しません．）この位相の関係は計算によって導かれましたが，その意味を直観的に考察しましょう．コイルに直流電源を繋ぎ，スイッチを入れた場合を考えます．スイッチを入れた瞬間，コイルには電源の起電力がかかり，最大限の外からの電位差がかかることになります．一方，自己誘導の起電力が逆向きに生じています．コイルの抵抗が無視できるものとすると，コイルにかかっている全体の電位差はオームの法則より $ 0[V]$ になります．この瞬間において，電流は $ 0[A]$ です．自己誘導が起こったとき，スイッチを入れた後，ゆっくりと電流は流れ始めるのでしたね．つまり，電位差（電源からの電位差です．）が先行し，電流は後からついてくることになります．今考えたことは，直流電源でスイッチを入れた瞬間の場合でした．流れ始めの位相の関係は交流でも同様で，その後の位相の関係もそのまま引き継ぐことになります．

　また，上に出てきた，

$\displaystyle \phi_{0}=\omega LI_{0}$

は最大値に関するオームの法則を表しています．ここで，

$\displaystyle \omega L$

という物理量は抵抗に相当するもので，リアクタンスといいます．さらに変形して，

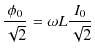  $\displaystyle \dfrac{\phi_{0}}{\sqrt{2}}=\omega L\dfrac{I_{0}}{\sqrt{2}}$    
% latex2html id marker 1789 $\displaystyle \therefore$ $\displaystyle \phi_{e}=\omega LI_{e}$    

となります．この式は実効値に関するオームの法則を示しています．

　次に，L回路における消費電力を考えてみましょう．消費電力の瞬時値 $ P(t)[W]$ を計算すると，

$\displaystyle P(t)$ $\displaystyle =I(t)\phi(t)$    
  $\displaystyle =I_{0}\sin\omega t\cdot\phi_{0}\cos\omega t$    
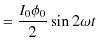  $\displaystyle =\dfrac{I_{0}\phi_{0}}{2}\sin⁡2\omega t$    

となります．この式から，時刻 $ 0[s]$ から，一周期後の時刻 $ T[s]$ までの時間平均 $ P[W]$ を計算してみます．

$\displaystyle P$ $\displaystyle =\dfrac{1}{T}\int_{0}^{T}P(t)dt$    
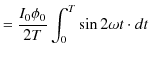  $\displaystyle =\dfrac{I_{0}\phi_{0}}{2T}\int_{0}^{T}\sin⁡2\omega t\cdot dt$    
  $\displaystyle =\dfrac{I_{0}\phi_{0}}{2T}[-\dfrac{\cos⁡2\omega t}{2\omega}]_{0}^{T}$    
  $\displaystyle =0$    

つまり，消費電力の時間平均は $ 0[J]$ です．エネルギーはコイルと交流電源の間を行き来していることになります．ここで，コイルに蓄えられているエネルギーの瞬時値 $ U(t)[J]$ を計算すると，

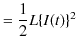$\displaystyle U(t)$ $\displaystyle =\dfrac{1}{2}L\{I(t)\}^{2}$    
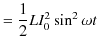  $\displaystyle =\dfrac{1}{2}LI_{0}^{2}\sin^{2}\omega t$    

となり，確かに周期的に増減を繰り返していることがわかります．

 

12.4 C回路

直流の場合，コンデンサーに電流が流れるのは，充電と放電のときだけでした．ここでは，コンデンサーに交流を流すことを考えます．交流電源にコンデンサーを1個だけ繋いだ回路をC回路と呼ぶことにします．C回路においては，電流と電位差の向きが時間とともに交互に入れ替わるので，充電と放電を繰り返すことに相当する現象が起こり，交流電流が常に流れることになります．交流電源の電位差が，

$\displaystyle \phi(t)=\phi_{0}\sin\omega t$

で変化するとき，電流はどのような式で表されるでしょうか？ 各時刻における電流の値は，短い時間間隔を $ \Delta t[s]$，その間に移動する電荷を $ \Delta Q(t)[C]$ として，

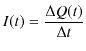
$\displaystyle I(t)=\dfrac{\Delta Q(t)}{\Delta t}$

と表されます．ここで，時間間隔 $ \Delta t[s]$ を限りなく 0 に近づける極限をとると，上式の右辺は時間についての微分になります．

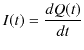
$\displaystyle I(t)=\dfrac{dQ(t)}{dt}$

また，電荷 $ Q(t)[C]$ は，電気容量を $ C[F]$ として，

$\displaystyle Q(t)$ $\displaystyle =C\phi(t)$    
  $\displaystyle =C\phi_{0}\sin⁡\omega t$    

です．よって，

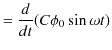$\displaystyle I(t)$ $\displaystyle =\dfrac{d}{dt}(C\phi_{0}\sin\omega t)$    
  $\displaystyle =\omega C\phi_{0}\cos\omega t$    

となります．ここで，電流の最大値を，

$\displaystyle I_{0}\equiv\omega C\phi_{0}$

とすると，電流の瞬時値は，

$\displaystyle I(t)=I_{0}\sin⁡(\omega t+\dfrac{\pi}{2})$

となります．この式から，電流の位相は電位差の位相より， $ \frac{\pi}{2}[rad]$ だけ大きい（進んでいる）ことがわかります．（位相のずれのため，瞬時値に関するオームの法則は成立しません．）この位相の関係は計算によって導かれましたが，その意味を直観的に考察しましょう．電荷の溜まっていないコンデンサーに直流電源を繋ぎ，スイッチを入れた場合を考えます．スイッチを入れた瞬間，コンデンサーは抵抗 $ 0[\Omega]$ の導線と同等であり，最大限の電流が流れます．一方，この瞬間において，溜まっている電荷が $ 0[C]$ なので，$ Q=C\phi$ より電位差も $ 0[V]$ です．つまり，電流が先行し，電位差は後からついてくることになります．今考えたことは，直流電源でスイッチを入れた瞬間の場合でした．流れ始めの位相の関係は交流でも同様で，その後の位相の関係もそのまま引き継ぐことになります．

　また，上で出てきた，

$\displaystyle I_{0}=\omega C\phi_{0}$

の式を変形すると，

$\displaystyle \phi_{0}=\dfrac{1}{\omega C}I_{0}$

となります．この式は最大値に関するオームの法則を表しています．ここで，

$\displaystyle \dfrac{1}{\omega C}$

という物理量は抵抗に相当するもので，リアクタンスといいます．さらに変形して，

  $\displaystyle \dfrac{\phi_{0}}{\sqrt{2}}=\dfrac{1}{\omega C}\cdot\dfrac{I_{0}}{\sqrt{2}}$    
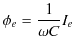% latex2html id marker 1860 $\displaystyle \therefore$ $\displaystyle \phi_{e}=\dfrac{1}{\omega C}I_{e}$    

となります．この式は実効値に関するオームの法則を示しています．

　次に，C回路におけるコンデンサーの消費電力を考えてみましょう．消費電力の瞬時値 $ P(t)[W]$ を計算すると，

$\displaystyle P(t)$ $\displaystyle =I(t)\phi(t)$    
  $\displaystyle =I_{0}\cos\omega t\cdot\phi_{0}\sin\omega t$    
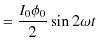  $\displaystyle =\dfrac{I_{0}\phi_{0}}{2}\sin⁡2\omega t$    

となります．この式から，時刻 $ 0[s]$ から，1周期後の時刻 $ T[s]$ までの時間平均 $ P[W]$ を計算してみます．

$\displaystyle P$ $\displaystyle =\dfrac{1}{T}\int_{0}^{T}P(t)dt$    
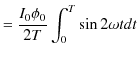  $\displaystyle =\dfrac{I_{0}\phi_{0}}{2T}\int_{0}^{T}\sin⁡2\omega tdt$    
  $\displaystyle =\dfrac{I_{0}\phi_{0}}{2T}[-\dfrac{\cos⁡2\omega t}{2\omega}]_{0}^{T}$    
  $\displaystyle =0$    

つまり，消費電力の時間平均は $ 0[J]$ です．エネルギーはコンデンサーと交流電源の間を行き来していることになります．ここで，コンデンサーに蓄えられているエネルギーの瞬時値 $ U(t)[J]$ を計算すると，

$\displaystyle U(t)$ $\displaystyle =\dfrac{1}{2}C\phi(t)^{2}$    
  $\displaystyle =\dfrac{1}{2}C\phi_{0}^{2}\sin^{2}\omega t$    

となり，確かに周期的に増減を繰り返していることがわかります．

 

12.5 RLC直列回路（交流電源がない場合）

コンデンサーを充電し，それをコイルに接続した場合，電位差と電流は時間とともに正弦的に振動します．このような現象を電気振動といいます．この回路で，コイルとコンデンサーでの電位差の瞬時値は等しく，また電流の瞬時値も等しくなります．（電流と電位差の瞬時値には位相のずれ $ \frac{\pi}{2}[rad]$ がありました．）コイルについて，最大値に関するオームの法則，

$\displaystyle \phi_{0}=\omega LI_{0}$

が成立します．一方，コンデンサーについて，最大値に関するオームの法則は，

$\displaystyle \phi_{0}=\dfrac{1}{\omega C}I_{0}$

です．これら2つの電位差の最大値は等しくなります．故に，電気振動の角振動数を $ \omega_{0}[rad/s]$ とすると，

  $\displaystyle \omega_{0}LI_{0}=\dfrac{1}{\omega_{0}C}I_{0}$    
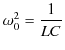% latex2html id marker 1896 $\displaystyle \therefore$ $\displaystyle \omega_{0}^{2}=\dfrac{1}{LC}$    
% latex2html id marker 1898 $\displaystyle \therefore$ $\displaystyle \omega_{0}=\dfrac{1}{\sqrt{LC}}$    

が求められます．電気振動はコイルの静磁エネルギー，

$\displaystyle U(t)=\dfrac{1}{2}L\{I(t)\}^{2}$

とコンデンサーの静電エネルギー，

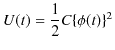
$\displaystyle U(t)=\dfrac{1}{2}C\{\phi(t)\}^{2}$

とが，お互いに入れ替わることによって生じていると考えることもできます．導線の電気抵抗が無視できるとき，エネルギーは保存するので，

$\displaystyle \dfrac{1}{2}LI_{0}^{2}=\dfrac{1}{2}L\{I(t)\}^{2}+\dfrac{1}{2}C\{\phi(t)\}^{2}=\dfrac{1}{2}C\phi_{0}^{2}$

が成立します．ここで，電気振動のアナロジーとして，水平ばね振り子を挙げておきます．水平ばね振り子では，運動エネルギー，

$\displaystyle \dfrac{1}{2}mv^{2}$

と，弾性エネルギー，

$\displaystyle \dfrac{1}{2}kx^{2}$

との間でエネルギーの交換が起こり，力学的エネルギーは保存します．このアナロジーではコイルの静磁エネルギーは運動エネルギーに，コンデンサーの静電エネルギーは弾性エネルギーに対応します．

　電気振動をRLC直列回路という広い視点から，微分方程式を使って一般的に取り扱ってみましょう．RLC直列回路とは，抵抗，コイル，コンデンサーと交流電源を直列に繋いだ回路を指します．交流電源がある場合をまず考えて，微分方程式を求めてみます．RLC直列回路に電流が流れ始めたときを考えます．このとき，抵抗には，

$\displaystyle RI(t)$

の電位差がかかります．また，コイルには外から電位差が，

$\displaystyle L\dfrac{dI(t)}{dt}$

だけかかります．（L回路のSectionを参照して下さい．）さらに，コンデンサーには，

$\displaystyle \dfrac{Q(t)}{C}$

の電位差が生じます．電位の高低の向きは全て同じです．この3つの電位差の合計と交流電源の起電力が等しくなります．したがって，交流電源の起電力が，

$\displaystyle \phi_{0}\sin\omega t$

で表される場合，

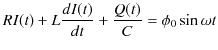
$\displaystyle RI(t)+L\dfrac{dI(t)}{dt}+\dfrac{Q(t)}{C}=\phi_{0}\sin\omega t$

が成立します．ここで，両辺を時間で微分すると，

$\displaystyle L\dfrac{d^{2}I(t)}{dt^{2}}+R\dfrac{dI(t)}{dt}+\dfrac{1}{C}\dfrac{dQ(t)}{dt}=\omega\phi_{0}\cos\omega t$

ですから，

$\displaystyle L\dfrac{d^{2}I(t)}{dt^{2}}+R\dfrac{dI(t)}{dt}+\dfrac{1}{C}I(t)=\omega\phi_{0}\cos\omega t$ (12.1)

となります．

　交流電源がない場合，(12.1)式で右辺を 0 とおいた同次方程式になります．

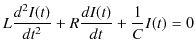
$\displaystyle L\dfrac{d^{2}I(t)}{dt^{2}}+R\dfrac{dI(t)}{dt}+\dfrac{1}{C}I(t)=0$

この微分方程式を，複素数を使った解法で解くことにしましょう．（この同次微分方程式は減衰振動の微分方程式，

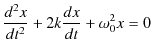
$\displaystyle \dfrac{d^{2}x}{dt^{2}}+2k\dfrac{dx}{dt}+\omega_{0}^{2}x=0$

と全く同形です．したがって，解法も同じです．）まず，

$\displaystyle \tilde{I}(t)\equiv I(t)+i\cdot J(t)$

と実数部と虚数部を持つ複素電流 $ \tilde{I}(t)$ を導入します．ここで，$ I(t)$ と $ J(t)$ は実数です．複素数の微分方程式，

$\displaystyle L\dfrac{d^{2}\tilde{I}(t)}{dt^{2}}+R\dfrac{d\tilde{I}(t)}{dt}+\dfrac{1}{C}\tilde{I}(t)=0$

を解き，その解の実数部がもとの微分方程式の解になります．このことは，複素数の微分方程式を変形して，

  $\displaystyle L\dfrac{d^{2}}{dt^{2}}(I(t)+iJ(t))+R\dfrac{d}{dt}(I(t)+iJ(t))+\dfrac{1}{C}(I(t)+iJ(t))=0$    
% latex2html id marker 1940 $\displaystyle \therefore$ $\displaystyle (L\dfrac{d^{2}I(t)}{dt^{2}}+R\dfrac{dI(t)}{dt}+\dfrac{1}{C}I(t))+i(L\dfrac{d^{2}J(t)}{dt^{2}}+R\dfrac{dJ(t)}{dt}+\dfrac{1}{C}J(t))=0$    

とすれば理解できます．ここで，

$\displaystyle \tilde{I}(t)\equiv\alpha\cdot e^{\lambda t}$

とおき直します．$ \alpha$ も $ \lambda$ も複素数です．このとき，

  $\displaystyle L\lambda^{2}\alpha e^{\lambda t}+R\lambda\alpha e^{\lambda t}+\dfrac{1}{C}\alpha e^{\lambda t}=0$    
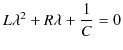% latex2html id marker 1949 $\displaystyle \therefore$ $\displaystyle L\lambda^{2}+R\lambda+\dfrac{1}{C}=0$    

ですが，最後の式の2次方程式を解くと，

$\displaystyle \lambda$ $\displaystyle =\dfrac{-R\pm\sqrt{R^{2}-\dfrac{4L}{C}}}{2L}$    
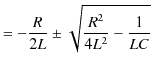  $\displaystyle =-\dfrac{R}{2L}\pm\sqrt{\dfrac{R^{2}}{4L^{2}}-\dfrac{1}{LC}}$    

となります．ルートの中の数の正負 0 により，3通りの場合分けが考えられます．

　最初に，$ R$ が小さい場合を取り扱います．すなわち，

$\displaystyle \dfrac{R^{2}}{4L^{2}}-\dfrac{1}{LC}<0$

の場合です．このとき，

$\displaystyle \lambda=-\gamma\pm i\omega'$

となります．ただし，

$\displaystyle \gamma$ $\displaystyle \equiv\dfrac{R}{2L}$    
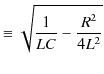$\displaystyle \omega'$ $\displaystyle \equiv\sqrt{\dfrac{1}{LC}-\dfrac{R^{2}}{4L^{2}}}$    

とおきました． $ \tilde{I}(t)$ は，

$\displaystyle \tilde{I}(t)=\alpha_{1}e^{-\gamma t}e^{i\omega' t}+\alpha_{2}e^{-\gamma t}e^{-i\omega' t}$

となります．ここで，複素数 $ \alpha_{1},\alpha_{2}$ を実数 $ a_{1},a_{2},b_{1},b_{2}$ を使って実数部と虚数部に分け，複素数の指数関数をオイラーの公式により，三角関数で表します．そして， $ \tilde{I}(t)$ を実数部と虚数部に分けます．

$\displaystyle \tilde{I}(t)$ $\displaystyle =(a_{1}+ib_{1})e^{-\gamma t}(\cos\omega' t+i\sin\omega' t)+(a_{2}+ib_{2})e^{-\gamma t}(\cos\omega' t-i\sin\omega' t)$    
  $\displaystyle =\{(-b_{1}+b_{2})e^{-\gamma t}\sin\omega' t+(a_{1}+a_{2})e^{-\gam... ..._{1}-a_{2})e^{-\gamma t}\sin\omega' t+(b_{1}+b_{2})e^{-\gamma t}\cos\omega' t\}$    

ここで，

$\displaystyle A_{1}$ $\displaystyle \equiv-b_{1}+b_{2}$    
$\displaystyle A_{2}$ $\displaystyle \equiv a_{1}+a_{2}$    

とおき，実数部をとって，同次微分方程式の解は次のようになります．

$\displaystyle I(t)$ $\displaystyle =A_{1}e^{-\gamma t}\sin\omega' t+A_{2}e^{-\gamma t}\cos\omega' t$    
  $\displaystyle =Ae^{-\gamma t}(a\sin\omega' t+b\cos\omega' t)\,(A_{1}\equiv Aa,A_{2}\equiv Ab)$    

ここで，

  $\displaystyle A'\equiv\sqrt{a^{2}+b^{2}}$    
  $\displaystyle \tan⁡\theta_{0}\equiv\dfrac{b}{a}$    

とおき，三角関数の公式を使うと，

$\displaystyle I(t)=Ae^{-\gamma t}A'\sin(\omega' t+\theta_{0})$

となります．さらに，

$\displaystyle I_{0}\equiv AA'$

とおくと，解は最終的に，

$\displaystyle I(t)=I_{0}e^{-\gamma t}\sin(\omega't+\theta_{0})$

となります．この式を見ると電流が振動していることがわかります．抵抗がある場合は，

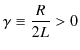
$\displaystyle \gamma\equiv\dfrac{R}{2L}>0$

となり，振動の振幅が時間とともに指数関数的に減少していきます．このような振動を減衰振動といいます．一方，抵抗が完全に $ 0[\Omega]$ の場合，

  $\displaystyle \gamma\equiv\dfrac{R}{2L}=0$    
  $\displaystyle \omega'\equiv\sqrt{\dfrac{1}{LC}-\dfrac{R^{2}}{4L^{2}}}=\dfrac{1}{\sqrt{LC}}(\equiv\omega_{0})$    

となるので，

$\displaystyle I(t)=I_{0}\sin(\omega_{0}t+\theta_{0})$

と表されるように単振動します．これが，このSectionで最初に初等的に取り扱った電気振動を表す式になります．

　次に，抵抗が大きい場合，すなわち，

$\displaystyle \dfrac{R^{2}}{4L^{2}}-\dfrac{1}{LC}>0$

の場合を考えましょう．このとき，

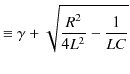$\displaystyle \lambda_{1}$ $\displaystyle \equiv\gamma-\sqrt{\dfrac{R^{2}}{4L^{2}}-\dfrac{1}{LC}}$    
$\displaystyle \lambda_{2}$ $\displaystyle \equiv\gamma+\sqrt{\dfrac{R^{2}}{4L^{2}}-\dfrac{1}{LC}}$    

とおくと，

$\displaystyle \tilde{I}(t)$ $\displaystyle =\alpha_{1}e^{-\lambda_{1}t}+\alpha_{2}e^{-\lambda_{2}t}$    
  $\displaystyle =(a_{1}+ib_{1})e^{-\lambda_{1}t}+(a_{2}+ib_{2})e^{-\lambda_{2}t}$    
  $\displaystyle =\{a_{1}e^{-\lambda_{1}t}+a_{2}e^{-\lambda_{2}t}\}+i\{b_{1}e^{-\lambda_{1}t}+b_{2}e^{-\lambda_{2}t}\}$    

なので，実数部をとり，解は，

$\displaystyle I(t)=a_{1}e^{-\lambda_{1}t}+a_{2}e^{-\lambda_{2}t}$

となります．電流は振動せずに指数関数的に減少しますが，これを過減衰といいます．

　最後に，

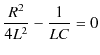
$\displaystyle \dfrac{R^{2}}{4L^{2}}-\dfrac{1}{LC}=0$

のときを考えましょう．このとき，

$\displaystyle \tilde{I}(t)$ $\displaystyle =\alpha e^{-\gamma t}$    
  $\displaystyle =(a+ib)e^{-\gamma t}$    
  $\displaystyle =ae^{-\gamma t}+ibe^{-\gamma t}$    

なので，実数部をとって，

$\displaystyle I(t)=ae^{-\gamma t}$

となります．しかし，2階線形微分方程式を取り扱っているので，このままでは一般解にはできません．そこで，

$\displaystyle I(t)=a(t)e^{-\gamma t}$

とおいてみます．このとき，時間微分して，

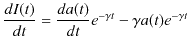
$\displaystyle \dfrac{dI(t)}{dt}=\dfrac{da(t)}{dt}e^{-\gamma t}-\gamma a(t)e^{-\gamma t}$

となります．さらに，もう一回時間微分して，

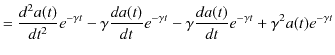$\displaystyle \dfrac{d^{2}I(t)}{dt^{2}}$ $\displaystyle =\dfrac{d^{2}a(t)}{dt^{2}}e^{-\gamma t}-\gamma\dfrac{da(t)}{dt}e^{-\gamma t}-\gamma\dfrac{da(t)}{dt}e^{-\gamma t}+\gamma^{2}a(t)e^{-\gamma t}$    
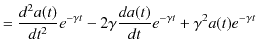  $\displaystyle =\dfrac{d^{2}a(t)}{dt^{2}}e^{-\gamma t}-2\gamma\dfrac{da(t)}{dt}e^{-\gamma t}+\gamma^{2}a(t)e^{-\gamma t}$    

となります．これらをもとの同次方程式，

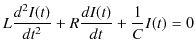
$\displaystyle L\dfrac{d^{2}I(t)}{dt^{2}}+R\dfrac{dI(t)}{dt}+\dfrac{1}{C}I(t)=0$

に代入すると，

  $\displaystyle L\{\dfrac{d^{2}a(t)}{dt^{2}}e^{-\gamma t}-2\gamma\dfrac{da(t)}{dt... ...t)}{dt}e^{-\gamma t}-\gamma a(t)e^{-\gamma t}\}+\dfrac{1}{C}a(t)e^{-\gamma t}=0$    
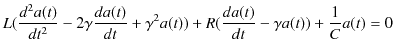% latex2html id marker 2031 $\displaystyle \therefore$ $\displaystyle L(\dfrac{d^{2}a(t)}{dt^{2}}-2\gamma\dfrac{da(t)}{dt}+\gamma^{2}a(t))+R(\dfrac{da(t)}{dt}-\gamma a(t))+\dfrac{1}{C}a(t)=0$    

となります．

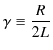
$\displaystyle \gamma\equiv\dfrac{R}{2L}$

ですから，

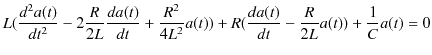  $\displaystyle L(\dfrac{d^{2}a(t)}{dt^{2}}-2\dfrac{R}{2L}\dfrac{da(t)}{dt}+\dfrac{R^{2}}{4L^{2}}a(t))+R(\dfrac{da(t)}{dt}-\dfrac{R}{2L}a(t))+\dfrac{1}{C}a(t)=0$    
% latex2html id marker 2036 $\displaystyle \therefore$ $\displaystyle L\dfrac{d^{2}a(t)}{dt^{2}}-L(\dfrac{R^{2}}{4L^{2}}-\dfrac{1}{LC})a(t)=0$    

となります．いま，

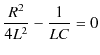
$\displaystyle \dfrac{R^{2}}{4L^{2}}-\dfrac{1}{LC}=0$

の場合を考えていたので，

  $\displaystyle \dfrac{d^{2}a(t)}{dt^{2}}=0$    
% latex2html id marker 2041 $\displaystyle \therefore$ $\displaystyle a(t)=At+B\,(A,B: const)$    

となり，一般解は，

$\displaystyle I(t)=(At+B)e^{-\gamma t}$

と表せます．やはり電流は振動せず指数関数的に減少することがわかります．この状態を臨界減衰といいます．

 

12.6 RLC直列回路（交流電源がある場合）

交流電源がある場合の，RLC直列回路を初等的に取り扱ってみましょう．（このSectionの後半は微分方程式による解法を見ていきます．）直列であるので抵抗，コイル，コンデンサーに流れる電流が共通になりますが，それを，

$\displaystyle I(t)=I_{0}\sin\omega t$

とおきます．このとき，R回路，L回路，C回路について，最大値に関するオームの法則と，電流と電位差の位相の関係より，R，L，Cにかかる電位差は次の式で表されます．

  $\displaystyle \phi_{R}(t)=RI_{0}\sin\omega t$    
  $\displaystyle \phi_{L}(t)=\omega LI_{0}\sin⁡(\omega t+\dfrac{\pi}{2})$    
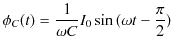  $\displaystyle \phi_{C}(t)=\dfrac{1}{\omega C}I_{0}\sin⁡(\omega t-\dfrac{\pi}{2})$    

電流と電位差の間の関係を，位相に注意しながら図に示します．

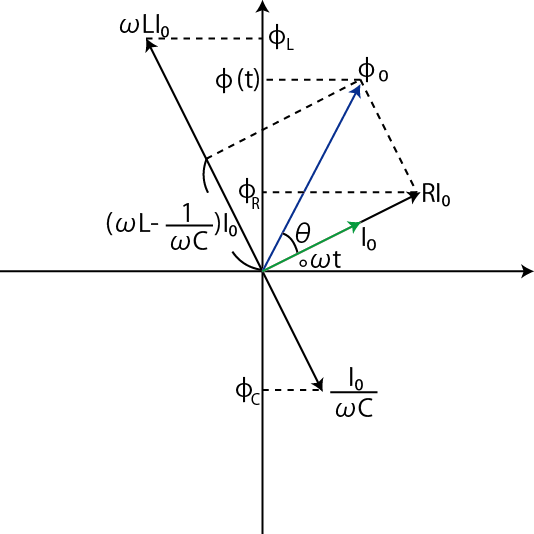
RLC直列回路

Figure12.2: RLC直列回路

この図より，交流電源の電位差の瞬時値は，

$\displaystyle \phi(t)=\phi_{0}\sin⁡(\omega t+\theta)$

で表されます．さらに，図より，

  $\displaystyle \phi_{0}^{2}=(RI_{0})^{2}+\{(\omega L-\dfrac{1}{\omega C})I_{0}\}^{2}$    
% latex2html id marker 2058 $\displaystyle \therefore$ $\displaystyle \phi_{0}^{2}=\{R^{2}+(\omega L-\dfrac{1}{\omega C})^{2}\}I_{0}^{2}$    
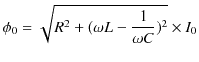% latex2html id marker 2060 $\displaystyle \therefore$ $\displaystyle \phi_{0}=\sqrt{R^{2}+(\omega L-\dfrac{1}{\omega C})^{2}}\times I_{0}$    

となります．ここで，

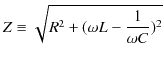
$\displaystyle Z\equiv\sqrt{R^{2}+(\omega L-\dfrac{1}{\omega C})^{2}}$

と定義します．この量はRLC直列回路の抵抗に相当するもので，インピーダンスといいます．このとき，

$\displaystyle \phi_{0}=ZI_{0}$

という最大値に関するオームの法則が成立します．また，電位差の位相と電流の位相の差を $ \theta[rad]$ とおくと，

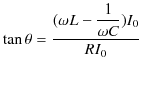  $\displaystyle \tan\theta=\dfrac{(\omega L-\dfrac{1}{\omega C})I_{0}}{RI_{0}}$    
% latex2html id marker 2069 $\displaystyle \therefore$ $\displaystyle \tan⁡\theta=\dfrac{\omega L-\dfrac{1}{\omega C}}{R}$    

の関係が成立します．ここで，抵抗が小さく，さらに，

$\displaystyle \omega L=\dfrac{1}{\omega C}$

が成立するとき，インピーダンスは微小になり，交流電流は極端に大きくなります．この現象が交流回路における共振と呼ばれるものです．

　それでは，交流電源がある場合のRLC直列回路について，微分方程式を使って取り扱ってみましょう．交流電源の起電力が，

$\displaystyle \phi(t)=\phi_{0}\sin⁡\omega t$

で表される場合，電流についての微分方程式は，

$\displaystyle L\dfrac{d^{2}I(t)}{dt^{2}}+R\dfrac{dI(t)}{dt}+\dfrac{1}{C}I(t)=\omega\phi_{0}\cos\omega t$ (12.2)

となることは，前のSectionで導出しました．線形微分方程式の解法の一般論にしたがい，右辺を 0 とおいた同次方程式，

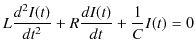
$\displaystyle L\dfrac{d^{2}I(t)}{dt^{2}}+R\dfrac{dI(t)}{dt}+\dfrac{1}{C}I(t)=0$

の解と(12.2)式の特解の和によって一般解を求めます．同次方程式の解は前のSectionでみたように，3つの場合についてそれぞれ求めました．次に，(12.2)式の特解を求めなくてはなりませんが，この方程式は抵抗力がある場合の強制振動の微分方程式，

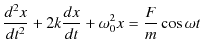
$\displaystyle \dfrac{d^{2}x}{dt^{2}}+2k\dfrac{dx}{dt}+\omega_{0}^{2}x=\dfrac{F}{m}\cos\omega t$

と同形であることに注意します．そのときと同じく，複素数を使った解法を採用することにします．(12.2)式の左辺の電流の代わりに複素電流，

$\displaystyle \tilde{I}(t)\equiv I(t)+iJ(t)$

を考え，右辺を，

$\displaystyle \omega\phi_{0}e^{i\omega t}$

とおき直します．このとき，

$\displaystyle L\dfrac{d^{2}\tilde{I}(t)}{dt^{2}}+R\dfrac{d\tilde{I}(t)}{dt}+\dfrac{1}{C}\tilde{I}(t)=\omega\phi_{0}e^{i\omega t}$

の微分方程式の解の実数部が(12.2)式の解になります．このことは，この複素数の微分方程式を変形して，

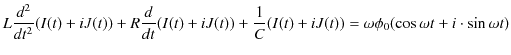  $\displaystyle L\dfrac{d^{2}}{dt^{2}}(I(t)+iJ(t))+R\dfrac{d}{dt}(I(t)+iJ(t))+\dfrac{1}{C}(I(t)+iJ(t))=\omega\phi_{0}(\cos\omega t+i\cdot\sin\omega t)$    
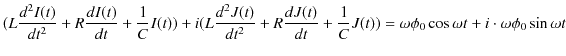% latex2html id marker 2089 $\displaystyle \therefore$ $\displaystyle (L\dfrac{d^{2}I(t)}{dt^{2}}+R\dfrac{dI(t)}{dt}+\dfrac{1}{C}I(t))+... ...}+\dfrac{1}{C}J(t))=\omega\phi_{0}\cos\omega t+i\cdot\omega\phi_{0}\sin\omega t$    

とすれば理解できます．さらに複素電流の角周波数は交流電源の角周波数 $ \omega[rad/s]$ に等しいので，

$\displaystyle \tilde{I}(t)=\tilde{I}_{0}e^{i\omega t}$

とおき直します． $ \tilde{I}_{0}$ も複素数で，この中に交流電源の電位差の位相と複素電流の位相とのずれがくりこまれることになります．複素電流を時間で微分していくと，

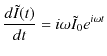  $\displaystyle \dfrac{d\tilde{I}(t)}{dt}=i\omega\tilde{I}_{0}e^{i\omega t}$    
% latex2html id marker 2098 $\displaystyle \therefore$ $\displaystyle \dfrac{d^{2}\tilde{I}(t)}{dt^{2}}=-\omega^{2}\tilde{I}_{0}e^{i\omega t}$    

となります．これらを微分方程式に代入して整理していきます．

  $\displaystyle -\omega^{2}L\tilde{I}_{0}e^{i\omega t}+i\omega R\tilde{I}_{0}e^{i\omega t}+\dfrac{1}{C}\tilde{I}_{0}e^{i\omega t}=\omega\phi_{0}e^{i\omega t}$    
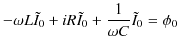% latex2html id marker 2101 $\displaystyle \therefore$ $\displaystyle -\omega L\tilde{I}_{0}+iR\tilde{I}_{0}+\dfrac{1}{\omega C}\tilde{I}_{0}=\phi_{0}$    
% latex2html id marker 2103 $\displaystyle \therefore$ $\displaystyle \{(-\omega L+\dfrac{1}{\omega C})+iR\}\tilde{I}_{0}=\phi_{0}$    
% latex2html id marker 2105 $\displaystyle \therefore$ $\displaystyle \tilde{I}_{0}=\dfrac{\phi_{0}}{(-\omega L+\dfrac{1}{\omega C})+iR}$    

最後の式の右辺の分母を複素インピーダンス，

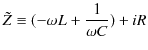
$\displaystyle \tilde{Z}\equiv(-\omega L+\dfrac{1}{\omega C})+iR$

と定義します．このとき，複素インピーダンスの絶対値は，

$\displaystyle Z$ $\displaystyle \equiv\vert\tilde{Z}\vert$    
  $\displaystyle =\sqrt{\vert\tilde{Z}\vert^{2}}$    
  $\displaystyle =\sqrt{\tilde{Z}^{*}\tilde{Z}}$    
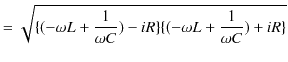  $\displaystyle =\sqrt{\{(-\omega L+\dfrac{1}{\omega C})-iR\}\{(-\omega L+\dfrac{1}{\omega C})+iR\}}$    
  $\displaystyle =\sqrt{(-\omega L+\dfrac{1}{\omega C})^{2}+R^{2}}$    
  $\displaystyle =\sqrt{R^{2}+(\omega L-\dfrac{1}{\omega C})^{2}}$    

となります．$ Z[\Omega]$ は実数ですが，初等的に考えたインピーダンスと一致していることが確認できます．ここで，複素平面上における複素インピーダンスの位相を $ \delta[rad]$ とおくと，

$\displaystyle \tilde{Z}=Ze^{i\delta}$

と表されます．ただし，

$\displaystyle \tan⁡\delta=\dfrac{R}{-\omega L+\dfrac{1}{\omega C}}$

です．以上より，

$\displaystyle \tilde{I}_{0}=\dfrac{\phi_{0}}{Ze^{i\delta}}$

となります．よって，

$\displaystyle \tilde{I}(t)$ $\displaystyle =\dfrac{\phi_{0}}{Ze^{i\delta}}e^{i\omega t}$    
  $\displaystyle =\dfrac{\phi_{0}}{Z}e^{i(\omega t-\delta)}$    
  $\displaystyle =\dfrac{\phi_{0}}{Z}\{\cos⁡(\omega t-\delta)+i\sin⁡(\omega t-\delta)\}$    

となります．実数部をとり，交流電流は，

$\displaystyle I(t)$ $\displaystyle =\dfrac{\phi_{0}}{Z}\cos⁡(\omega t-\delta)$    
  $\displaystyle =\dfrac{\phi_{0}}{Z}\sin\{\omega t-(\delta-\dfrac{\pi}{2})\}$    

となります．交流電源の電位差が，

$\displaystyle \phi(t)=\phi_{0}\sin\omega t$

だったことを思い出すと，

$\displaystyle \theta\equiv\delta-\dfrac{\pi}{2}$

が電位差と電流の位相差になっていることがわかります．このとき，

$\displaystyle \tan⁡\theta$ $\displaystyle =\tan(\delta-\dfrac{\pi}{2})$    
  $\displaystyle =-\cot\delta$    
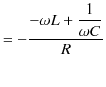  $\displaystyle =-\dfrac{-\omega L+\dfrac{1}{\omega C}}{R}$    
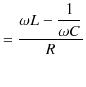  $\displaystyle =\dfrac{\omega L-\dfrac{1}{\omega C}}{R}$    

となり，このSectionの最初に取り扱った初等的議論の結果と一致することが確認されます．また，交流電源の電位差の位相を $ \omega t[rad]$ とした場合，電流の位相が $ \omega t-\theta[rad]$ となることがわかりました．これを初等的議論の結果と完全に合わせるためには，交流電源の電位差の位相も電流の位相も $ \theta[rad]$ だけ進めればよいです．このとき，交流電源の電位差の位相は $ \omega t+\theta[rad]$ であり，直列回路共通の電流の位相は $ \omega t[rad]$ となります．