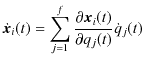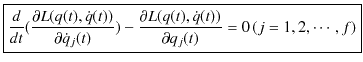Part1 解析力学の成立
Chapter1 ラグランジアン形式
1.1 一般化座標
通常,デカルト座標においては,1つの質点の座標ベクトルは,
で表されます.![]() は,座標ベクトルとその成分が,時間の関数で,時間とともに変化することを示しています.この座標を他の座標系で表すことができます.例えば,球面座標では次のようになります.
は,座標ベクトルとその成分が,時間の関数で,時間とともに変化することを示しています.この座標を他の座標系で表すことができます.例えば,球面座標では次のようになります.
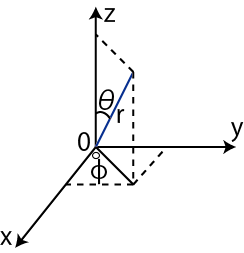
Figure1.1: 球面座標
この場合,
![]() で座標を表すことになります.このような様々な座標を一般化して,
で座標を表すことになります.このような様々な座標を一般化して,
とおくことにします.この座標を一般化座標といいます.このとき,デカルト座標での座標ベクトルと一般化座標は,次のように一般的に関係付けられます.
ここで,![]() 個の質点から構成される質点系を取り扱ってみましょう.この場合の自由度,すなわち座標の数は,
個の質点から構成される質点系を取り扱ってみましょう.この場合の自由度,すなわち座標の数は,![]() です.故に,一般化座標は,
です.故に,一般化座標は,
と拡張されます.例えば,![]() 番目
番目
![]() の質点のデカルト座標での座標ベクトル
の質点のデカルト座標での座標ベクトル
![]() を,一般化座標で表すと,
を,一般化座標で表すと,
となります.このとき,座標ベクトルの時間微分は,
です.ただし,ドットは時間の常微分を示します.
1.2 ラグランジアン
![]() 質点系を取り扱う際,系全体を記述する量として,次のラグランジアン
質点系を取り扱う際,系全体を記述する量として,次のラグランジアン ![]() という物理量を定義します.
という物理量を定義します.
ここで,![]() は系全体の運動エネルギー,
は系全体の運動エネルギー,![]() は系全体のポテンシャルです.すなわち,
は系全体のポテンシャルです.すなわち,
 |
||
です.(1.1)式と(1.2)式より,![]() と
と ![]() は一般化座標を用いて,次のように表されます.
は一般化座標を用いて,次のように表されます.
したがって,ラグランジアンは一般化座標を用いて,次のように表されます.
ここで,
![]() は
は ![]() 個の独立した変数です.また,最右辺の式は,変数を簡略化して表したものです.
個の独立した変数です.また,最右辺の式は,変数を簡略化して表したものです.
1.3 ハミルトンの原理(変分原理)
光がレンズなどの媒質に入射して屈折する際,屈折の法則が成立します.と同時に,実はもう1つ別の原理が成立しています.それは,光が進行するときに,最小の時間で済む経路を選択するというものです.これをフェルマーの原理といいます.光は,すなわち自然は,最小の時間で済む経路を知っているのです.この原理を力学に拡張しましょう.まず,![]() 質点系について時間が
質点系について時間が ![]() から
から ![]() へ経過するとき,次の作用と呼ばれる物理量
へ経過するとき,次の作用と呼ばれる物理量
![]() を,系を記述するラグランジアンから定義します.
を,系を記述するラグランジアンから定義します.
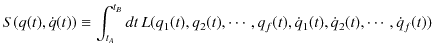
このとき,![]() 個の質点からなる系全体は,作用
個の質点からなる系全体は,作用
![]() が最小になるように運動します.自然はこのことを知っているのです.この原理のことを,最小作用の原理といいます.
が最小になるように運動します.自然はこのことを知っているのです.この原理のことを,最小作用の原理といいます.
最小作用の原理を実際に数学的に表現するためには,ハミルトンの原理(変分原理)といわれる原理を使います.作用
![]() は
は
![]() の関数になっていますが,
の関数になっていますが,
![]() はそれぞれ時間の関数です.関数の関数のことを汎関数といいます.この場合,関数
はそれぞれ時間の関数です.関数の関数のことを汎関数といいます.この場合,関数
![]() の関数である作用
の関数である作用
![]() が汎関数です.ハミルトンの原理(変分原理)とは,
が汎関数です.ハミルトンの原理(変分原理)とは,
原理1.1(ハミルトンの原理(変分原理)) "汎関数である作用
![]() が,最大または最小の停留値をとるような運動が実現します."
が,最大または最小の停留値をとるような運動が実現します."
という原理です.作用
![]() が最小値をとるような運動が実現するということは,最小作用の原理にほかなりません.単なる関数の極値を求める問題は微分により解くことができますね.これに対して,関数の関数である汎関数が停留値をとる問題を解くには変分といわれるものを使います.
が最小値をとるような運動が実現するということは,最小作用の原理にほかなりません.単なる関数の極値を求める問題は微分により解くことができますね.これに対して,関数の関数である汎関数が停留値をとる問題を解くには変分といわれるものを使います.
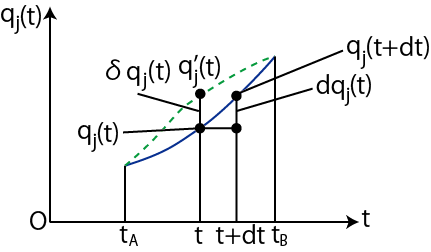
Figure1.2: ハミルトンの原理(変分原理)
図に示しているように,時刻 ![]() と時刻
と時刻 ![]() における座標は固定しています.そして,その間の座標の変化をある関数
における座標は固定しています.そして,その間の座標の変化をある関数
![]() で表します.(時間微分は,
で表します.(時間微分は,
![]() です.)この場合の作用
です.)この場合の作用 ![]() は,
は,
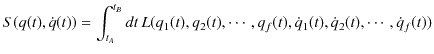
です.次に時刻 ![]() と時刻
と時刻 ![]() における座標値は変えずに,その途中の座標の値を少しだけ変えて,軌道を図の破線のようにして,その関数を
における座標値は変えずに,その途中の座標の値を少しだけ変えて,軌道を図の破線のようにして,その関数を ![]() とします.(時間微分の関数は,
とします.(時間微分の関数は,
![]() とします.)
とします.)
![]() の関数形を変えたのです.この場合の作用
の関数形を変えたのです.この場合の作用
![]() は,
は,
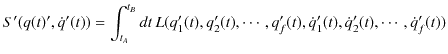
となります.
![]() の変化を,
の変化を,
と表しておきます.(図を見て下さい.)関数の微小差
![]() を変分といいます.(同一関数の時間変化に対する値の差である微分,
を変分といいます.(同一関数の時間変化に対する値の差である微分,
との違いに注意して下さい.(図を見て下さい.))変分をとったときの作用の変化
![]() は,
は,
と表せます.ハミルトンの原理(変分原理)は,
を要求します.これは,関数の微小な変化,つまり変分
![]() に対して,作用
に対して,作用
![]() が値を変えない,つまり停留値をとっていることを意味しています.この条件を満たすように,質点系の運動は決定されるのです.
が値を変えない,つまり停留値をとっていることを意味しています.この条件を満たすように,質点系の運動は決定されるのです.
1.4 オイラー-ラグランジュ方程式
前Sectionのハミルトンの原理(変分原理)より,ラグランジアン形式の基礎方程式を導出しましょう.以下のように,
![]() を計算していきます.
を計算していきます.
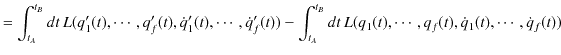 |
||
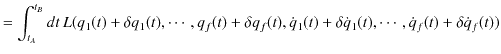 |
||
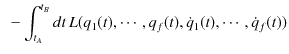 |
||
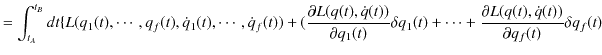 |
||
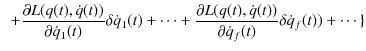 |
||
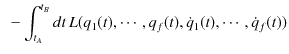 |
||
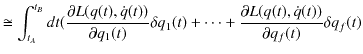 |
||
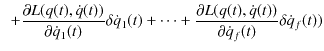 |
最後の変形では,2次の微小量は省略しました.また,
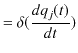 |
||
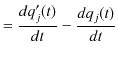 |
||
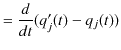 |
||
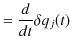 |
が成立します.計算を続けます.
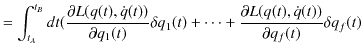 |
||
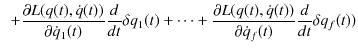 |
||
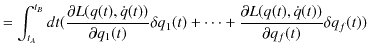 |
||
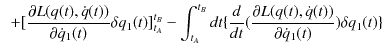 |
||
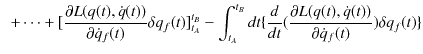 |
最後の変形には部分積分を使いました.ここで,始点と終点は固定されているので,
です.故に,
 |
||
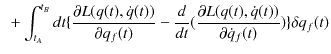 |
となります.ここで,ハミルトンの原理より,
ですので,
が成立します.この(1.3)式をオイラー-ラグランジュ方程式といいます.ラグランジアン形式の中心となる方程式です.
ここで,1質点の場合,確かにオイラー-ラグランジュ方程式からニュートンの運動方程式が導かれることを確認しておきましょう.一般化座標としてデカルト座標
![]() をとり,質点の質量を
をとり,質点の質量を ![]() ,ポテンシャルを
,ポテンシャルを
![]() とします.このとき,ラグランジアン
とします.このとき,ラグランジアン
![]() は,
は,
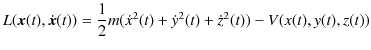
です.![]() 成分について調べると,
成分について調べると,
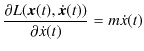 |
||
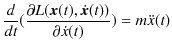 |
となり,また,
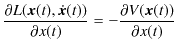
であるので,オイラー-ラグランジュ方程式(1.3)式は,
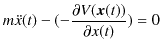 |
||
となります.確かに運動方程式が導かれました.![]() 成分と
成分と ![]() 成分についても同様です.
成分についても同様です.